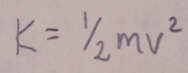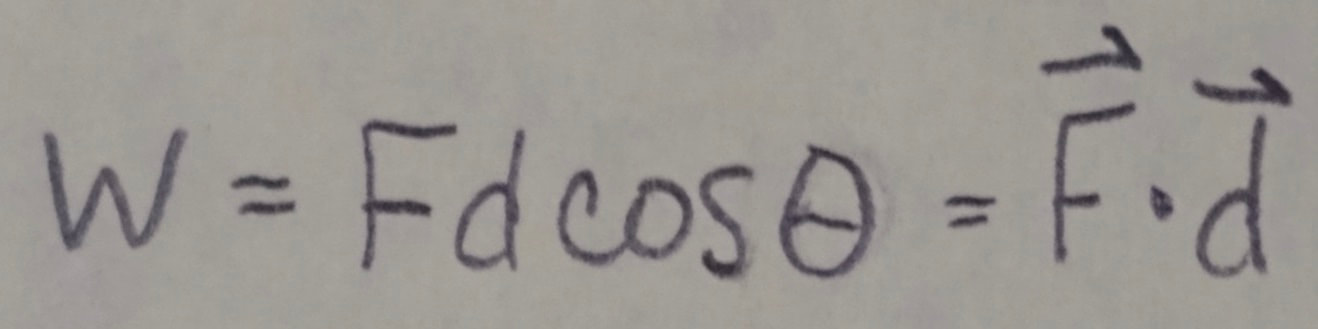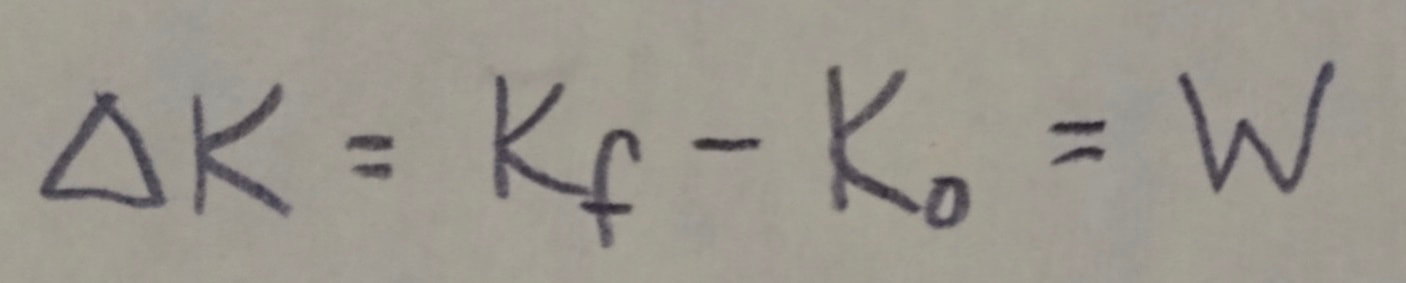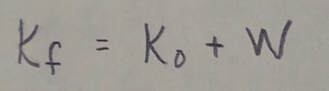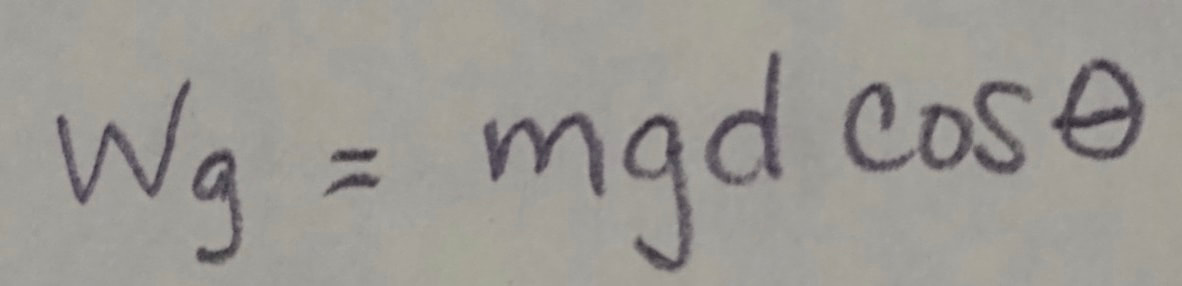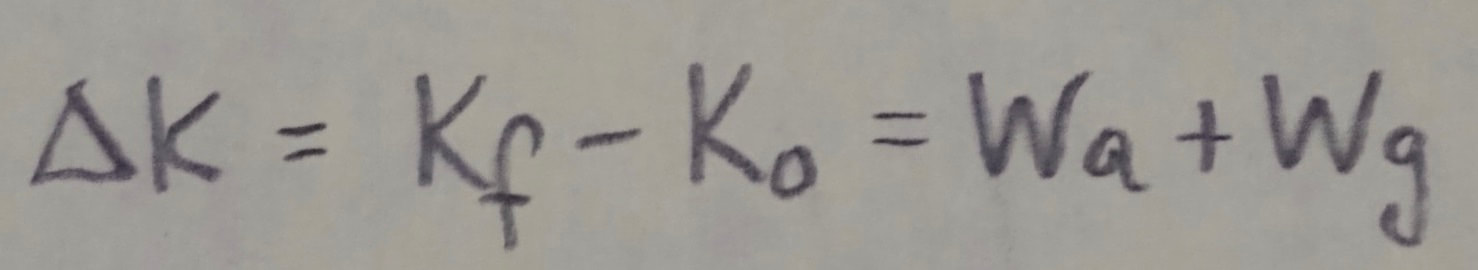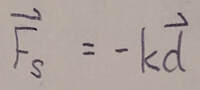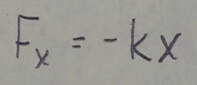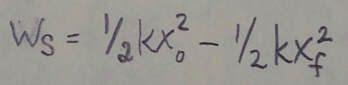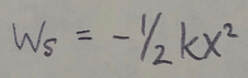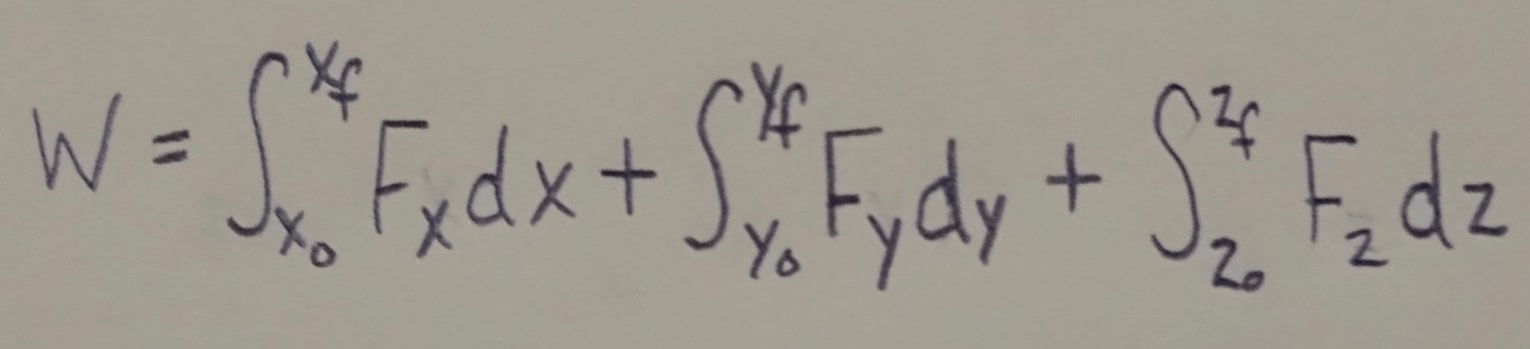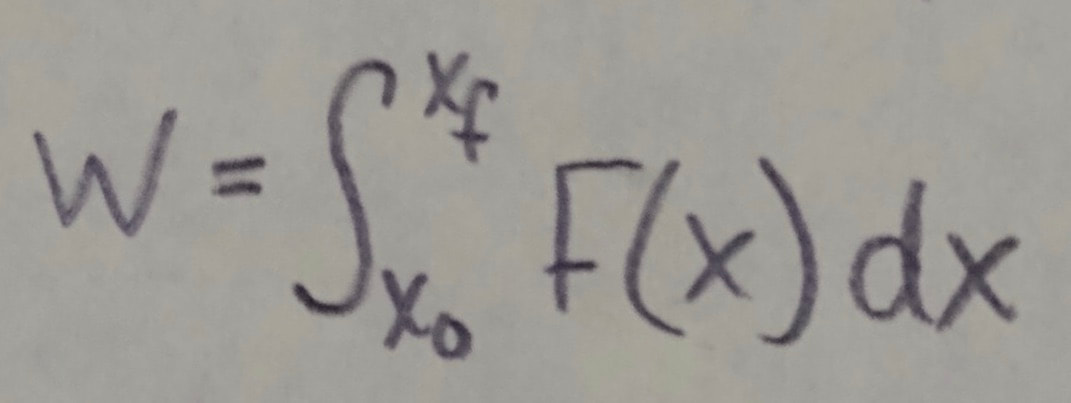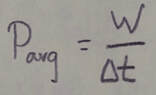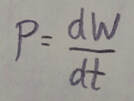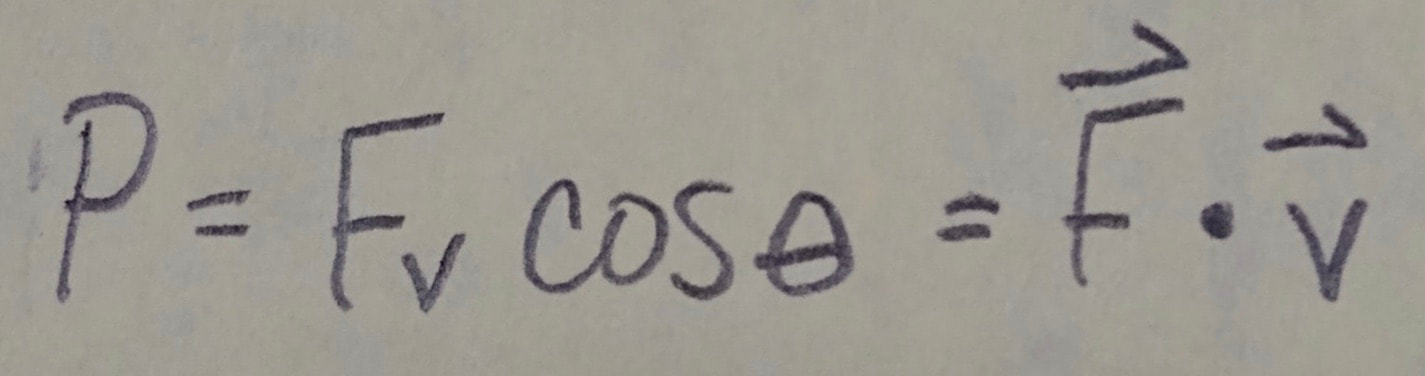Kinetic Energy and Work
|
Kinetic Energy: The kinetic energy K associated with the motion of a particle of mass m and speed v, where v is well below the speed of light, is:
Work: Work W is energy transferred to or from an object via a force acting on the object. Energy transferred to the object is positive work, and from the object, negative work.
Work Done by a Constant Force: The work done on a particle by a constant force F during displacement d is:
in which theta is the constant angle between the directions of F and d. Only the component of F that is along the displacement d can do work on the object. When two or more forces act on the object, their net work is the sum of the individual works done by the forces, which is also equal to the work that would be done on the object by the net force F(sub)net of those forces.
Work and Kinetic Energy: For a particle, a change (delta K) in the kinetic energy equals the net work W done on the particle:
in which K(sub)o is the original kinetic energy of the particle and K(sub)f is the final kinetic energy after the work is done. Rearranging the previous equation gives us:
Work Done by Gravitational Force: The work W(sub)g done by the gravitational force F(sub)g on a particle-like object of mass m as the object moves through a displacement d is given by:
in which theta is the angle between F(sub)g and d.
If K(sub)f = K(sub)o, then the above equation reduces to:
which tells us that applied force transfers as much energy to the object as the gravitational force transfers from it.
Spring Force: The force, F(sub)s, from a spring is:
|
(continued from previous column) where d is the displacement of the spring's free end from its position when the spring is in its relaxed state (neither compressed nor extended), and k is the spring constant (a measure of the spring's stiffness). If an x-axis lies along the spring, with the origin at the location of the spring's free end when the spring is in its relaxed state, the previous equation can be written as:
(Hooke's Law)
A spring force is thus a variable force: It varies with the displacement of the spring's free end. Work Done by a Spring Force: If an object is attached to the spring's free end, the work, W(sub)s, done on the object by the spring force when the object is moved from an initial position x(sub)o to a final position x(sub)f is:
Work Done by a Variable Force: When the force F on a particle-like object depends on the position of the object, the work done by F on the object while the object moves from an initial position r(sub)0 with coordinates x(sub)0, y(sub)0, and z(sub)0 to a final position r(sub)f with coordinates x(sub)f, y(sub)f, and z(sub)f must be found by integrating the force. If we assume that component F(sub)x may depend on x but not on y or z, component F(sub)y may depend on y but not on x or z, and component F(sub)z may depend on z but not on x or y, then the work is:
If F has only an x component, then the equation above becomes:
Power: The power due to force is the rate at which that force does work on an object. If the force does work W during a time interval delta t, the average power due to the force over the time interval is:
Instantaneous power is the instantaneous rate of doing work:
For a force F at an angle theta to the direction of travel of the instantaneous velocity v, the instantaneous power is:
|
Files:
| APCM Chapter 7 Presentation | |
| File Size: | 5722 kb |
| File Type: | ppt |