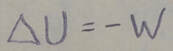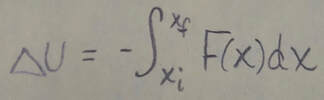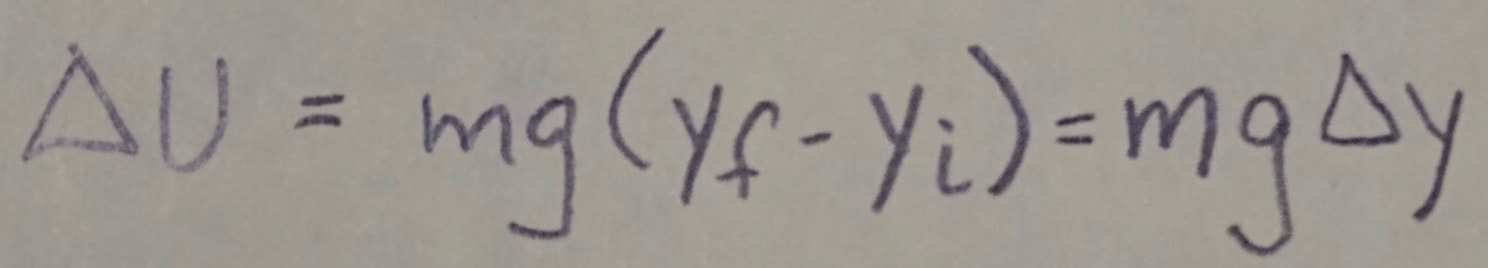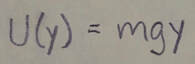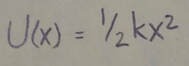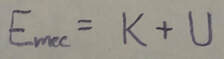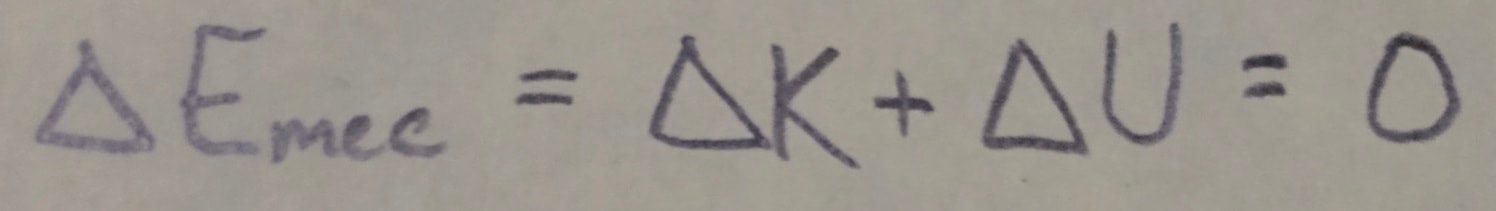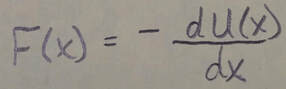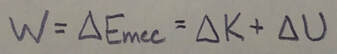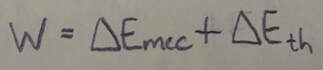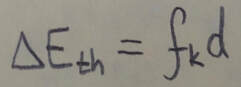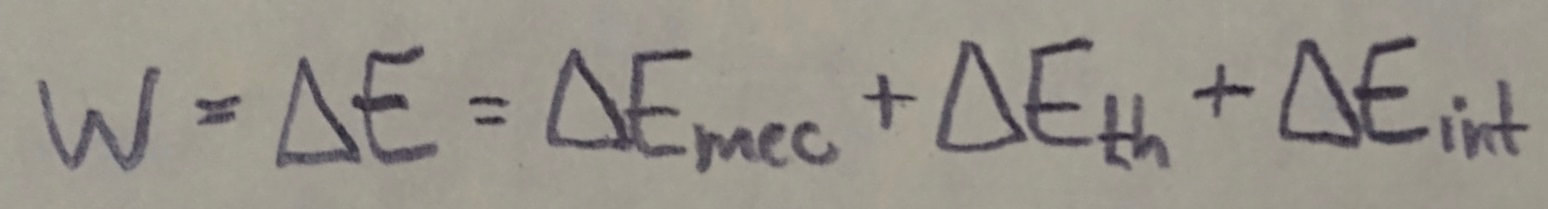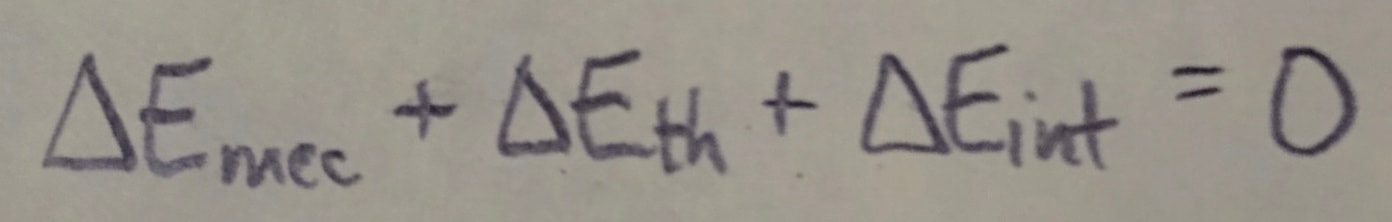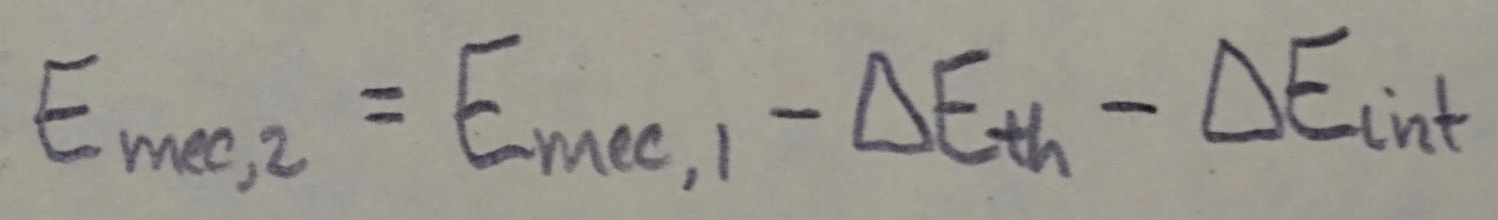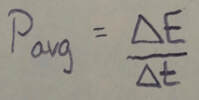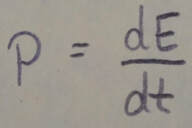Potential Energy and Conservation
|
Conservative Forces: A force is a conservative force if the net work it does on a particle moving around any closed path, from an initial point and then back to that point, is zero. Equivalently, a force is conservative if the net work it does on a particle moving between two points does not depend on the path taken by the particle. The gravitational force and the spring force are conservative forces; the kinetic frictional force is a nonconservative force.
Potential Energy: Potential energy is energy that is associated with the configuration of a system in which a conservative force acts. When the conservative force does work W on a particle within the system, the change delta U in the potential energy of the system is:
If the particle moves from point x(sub)i to point x(sub)f, the change in the potential energy of the system is:
Gravitational Potential Energy: The potential energy associated with a system consisting of Earth and a nearby particle is gravitational potential energy. If the particle moves from height y(sub)i to height y(sub)f, the change in the gravitational potential energy of the particle-Earth system is:
If the reference point of the particle is set as y(sub)i = 0 and the corresponding gravitational potential energy of the system is set as U(sub)i = 0, then the gravitational potential energy U when the particle is at any height y is:
Elastic Potential Energy: Elastic potential energy is the energy associated with the state of compression or extension of an elastic object. For a spring that exerts a spring force F = -kx when its free end has displacement x, the elastic potential energy is:
The reference configuration has the spring at its relaxed length, at which x = 0 and U = 0.
Mechanical Energy: The mechanical energy E(sub)mec of a system is the sum of all its kinetic energy K and potential energy U.
An isolated system is one in which no external force causes energy changes. If only conservative forces do work within an isolated system, then the mechanical energy E(sub)mec of the system cannot change. This principle of conservation of mechanical energy is written as:
in which the subscripts refer to different instants during an energy transfer process. This conservation principle can also be written as:
|
Potential Energy Curves: If we know the potential energy function U(x) for a system in which a one-dimensional force F(x) acts on a particle, we can find the force as:
If U(x) is given on a graph, then at any value of x, the force F(x) is the negative of the slope of the curve there and the kinetic energy of the particle is given by:
where E(sub)mec is the mechanical energy of the system. A turning point is a point x at which the particle reverses its motion (there, K = 0). The particle is in equilibrium at points where the slope of the U(x) curve is zero (there, F(x) = 0).
Work Done on a System by an External Force: Work W is energy transferred to or from a system by means of an external force acting on the system. When more than one force acts on a system, their net work is the transferred energy. When friction is not involved, the work done on the system and the change delta E(sub)mec in the mechanical energy of the system are equal:
When a kinetic frictional force acts within the system, then the thermal energy E(sub)th of the system changes. (This energy is associated with the random motion of atoms and molecules in the system.). The work done on the system is then:
The change delta E(sub)th is related to the magnitude f(sub)k of the frictional force and the magnitude d of the displacement caused by the external force by:
Conservation of Energy: The total energy E of a system (the sum of its mechanical energy and its internal energies, including thermal energy) can change only by amounts of energy that are transferred to or from the system. This experimental fact is known as the law of conservation of energy. If work W is done on the system, then:
If the system is isolated (W = 0), this gives:
and
where the subscripts 1 and 2 refer to two different instants.
Power: The power due to a force is the rate at which that force transfers energy. If an amount of energy delta E is transferred by a force in an amount of time delta t, the average power of the force is:
The instantaneous power due to a force is:
|
Files:
| APCM Chapter 8 Presentation | |
| File Size: | 4440 kb |
| File Type: | ppt |