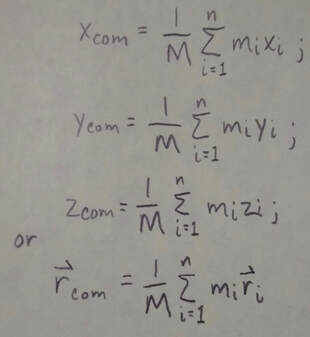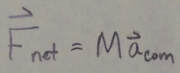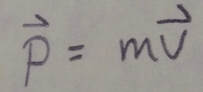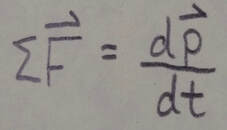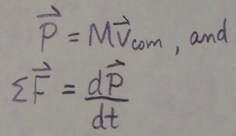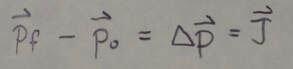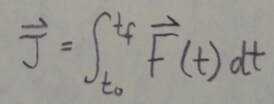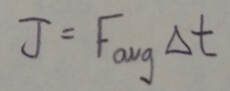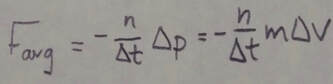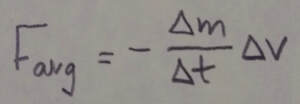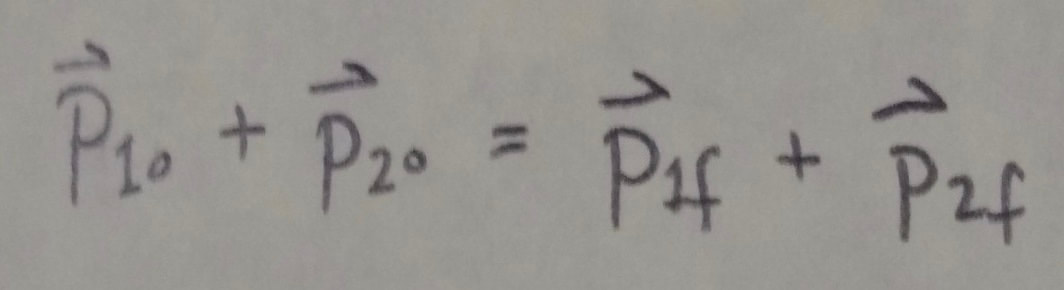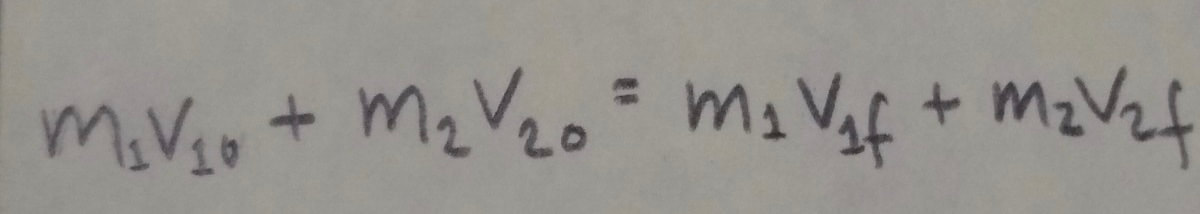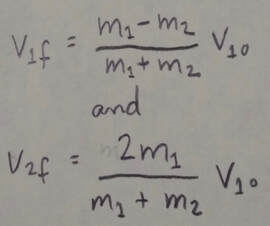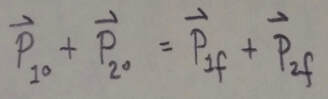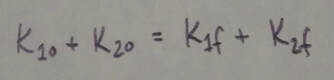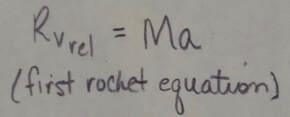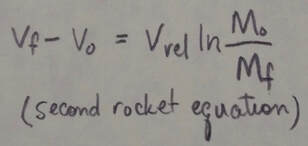Center of Mass and Linear Momentum
|
Center of Mass: The center of mass of a system of n particles is defined to be the point whose coordinates are given by:
where M is the total mass of the system.
Newton's second Law for a System of Particles: The motion of the center of mass of any system of particles is governed by Newton's second law for a system of particles, which is:
Here F(sub)net is the net force of all the external forces acting on the system, M is the total mass of the system, and a(sub)com is the acceleration of the system's center of mass.
Linear Momentum and Newton's Second Law: For a single particle, we define a quantity p, called its linear momentum as:
and can write Newton's second law in terms of this momentum:
For a system of particles these relations become:
Collision and Impulse: Applying Newton's second law in momentum form to a particle-like body involved in a collision leads to the impulse-linear momentum theorem:
Where final momentum - original momentum is the change in the body's linear momentum and J is the impulse due to the force F(t) exerted on the body by the other body in the collision:
If F(sub)avg is the average magnitude of F(t) during the collision and delta t is the duration of the collision, then for one-dimensional motion:
When a steady stream of bodies, each with mass m and speed v, collides with a body whose position is fixed, the average force on the fixed body is:
where n/delta t is the rate at which the bodies collide with the fixed body, and delta v is the change in velocity of each colliding body. This average force can also be written as:
where delta m/delta t is the rate at which mass collides with the fixed body. In the previous two equations, delta v = -v if the bodies stop upon impact and delta v = -2v is they bounce directly backward with no change in their speed.
Conservation of Linear Momentum: If a system is isolated so that no net external force acts on it, the linear momentum P of the system remains constant:
|
this can also be written as:
where the subscripts refer to the values of P at some original time and at a later time. The two statements above are equivalent statements of the law of conservation of linear momentum.
Inelastic Collision in One Dimension: In an inelastic collision of two bodies, the kinetic energy of the two-body system is not conserved. If the system is closed and isolated, the total linear momentum of the system must be conserved, which we can write in vector form as:
where subscripts o and f refer to values just before and just after the collision, respectively(symbols for single objects are lowercase, symbols for systems of particles are capital letters, the above is lowercase, further down is capital).
If the motion of the bodies is along a single axis, the collision is one-dimensional and we can rewrite the previous equation in terms of velocity components along that axis: If the bodies stick together, the collision is completely inelastic and the bodies have the same final velocity V (because they are stuck together).
Motion of the Center of Mass: The center of mass of a closed, isolated system of two colliding bodies is not affected by a collision. In particular, the velocity v(sub)com of the center of mass cannot be changed by the collision.
Elastic Collisions in One Dimension: An elastic collision is a special type of collision in which the kinetic energy of a system of colliding bodies is conserved. If the system is closed and isolated, its linear momentum is also conserved. For a one-dimensional collision in which body 2 is a target and body 1 is an incoming projectile, conservation of kinetic energy and linear momentum yield the following expressions for the velocities immediately after the collision:
Collisions in Two Dimensions: If two bodies collide and their motion is not along a single axis (the collision is not head-on), the collision is two-dimensional. If the two body system is closed and isolated, the law of conservation of momentum applies to the collision and can be written as:
In component form, the law gives two equations that describe the collision (one equation for each of the two dimensions). If the collision is also elastic (a special case), the conservation of kinetic energy during the collision gives a third equation:
Variable-Mass Systems: In the absence of external forces a rocket accelerates at an instantaneous rate given by:
in which M is the rocket's instantaneous mass (including unexpended fuel), R is the fuel consumption rate, and v(sub)rel is the fuel's exhaust speed relative to the rocket. The term Rv(sub)rel is the thrust of the rocket engine. For a rocket with constant R and v(sub)rel, whose speed changes from v(sub)0 to v(sub)f when its mass changes from M(sub)0 to M(sub)f (ln is natural log):
|
Files:
| APCM Chapter 9 Presentation | |
| File Size: | 6418 kb |
| File Type: | ppt |