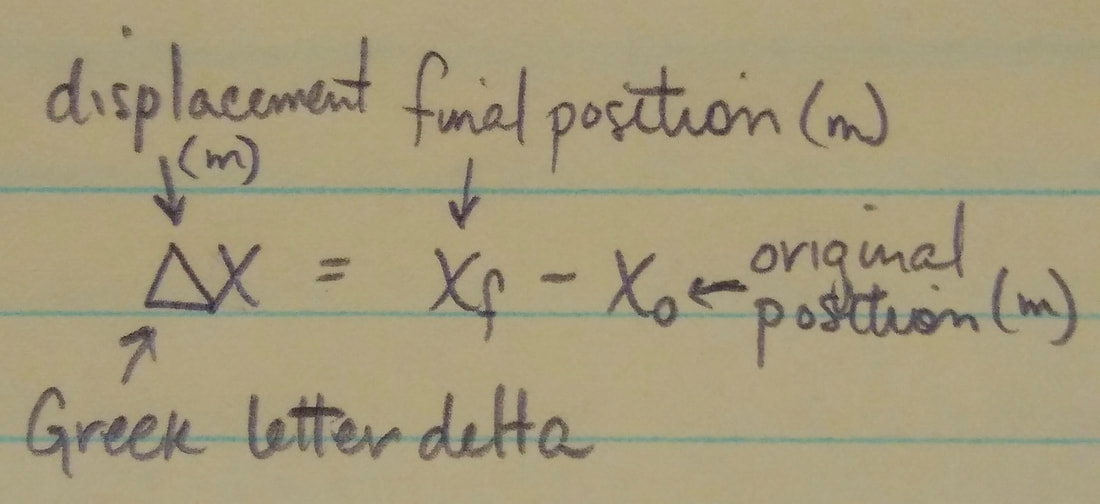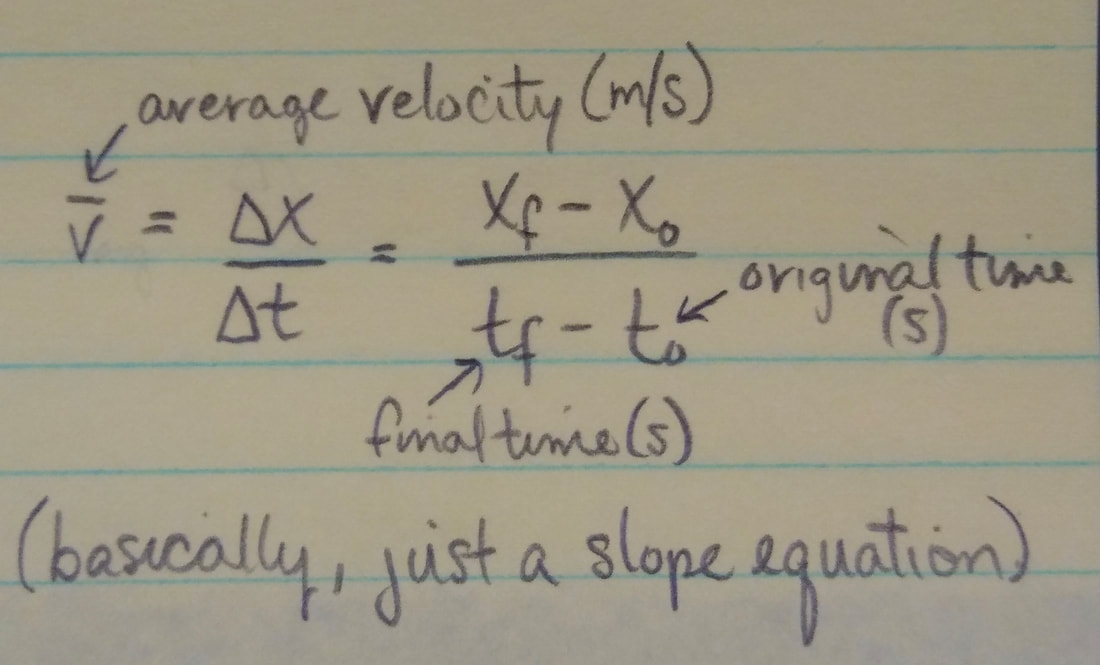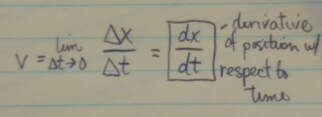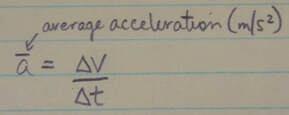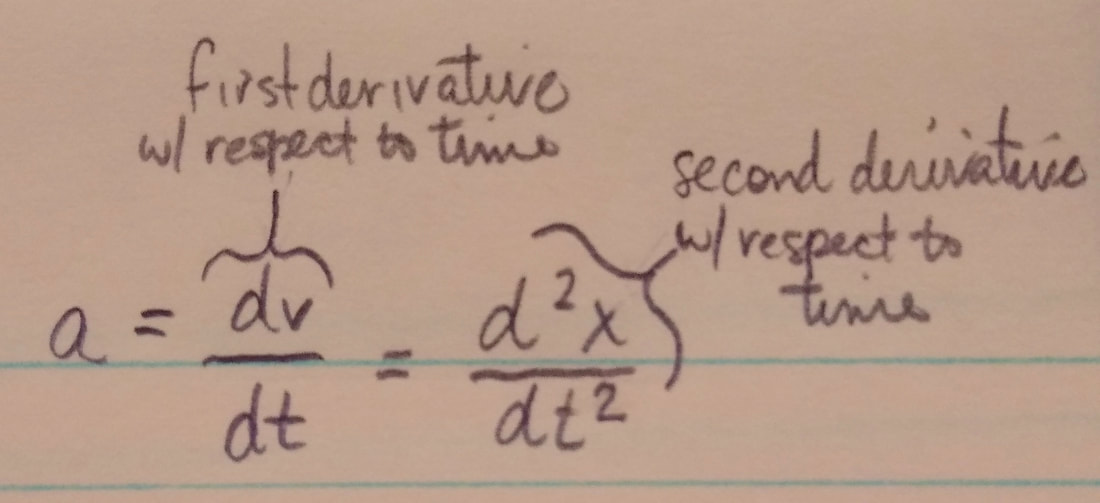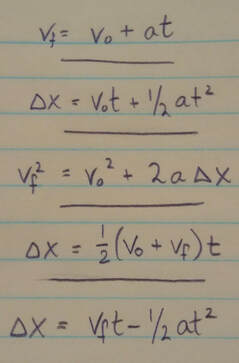Motion Along a Straight Line
|
Position: The position (x) of a particle on an x axis locates the particle with respect to the origin, or zero point, of the axis. The position is either positive or negative, according to which side of the origin the particle is on, or zero if the particle is at the origin. The positive direction on an axis is the direction of increasing positive numbers; the opposite direction is the negative direction on the axis.
Displacement: The displacement (delta x) of a particle is the change in its position:
Displacement is a vector quantity. It is positive if the particle has moved in the positive direction of the x axis and negative if the particle has moved in the negative direction.
Average velocity: When a particle has move from position x1 to position x2 during a time interval delta t = t2 - t1, its average velocity during that interval is:
The algebraic sign of v-avg indicates the direction of motion (v-avg is a vector quantity). Average velocity does not depend on the actual distance a particle moves, but instead depends on its original and final positions.
-On a graph of x versus t, the average velocity for a time interval delta t is the slope of the straight line connecting the points on the curve that represent the two ends of the interval. Average speed: The average speed (s) of a particle during a time interval delta t depends on the total distance the particle moves in that time interval:
Instantaneous Velocity: The instantaneous velocity (or simply velocity) v of a moving particle is:
|
(continued from previous column) where delta x and delta t are defined in the average velocity equation. The instantaneous velocity (at a particular time) may be found as the slope (at that particular time) of the graph of x versus t. Speed is the magnitude of instantaneous velocity.
Average acceleration: Average acceleration is the ratio of a change in velocity (delta v) to the time interval delta t in which the change occurs:
The algebraic sign indicated the direction of a-avg.
Instantaneous Acceleration: Instantaneous acceleration (or simply acceleration) a is the first time derivative of velocity v(t) and the second time derivative of position x(t):
On a graph of v versus t, the acceleration (a) at any time (t) is the slope of the curve at the point that represents t.
Constant acceleration: The five major kinematics equations in physics describe the motion of a particle with constant acceleration:
These are not valid when the acceleration is not constant.
Free-Fall Acceleration: An important example of straight-line motion with constant acceleration is that of an object rising or falling freely near Earth's surface. The constant acceleration equations describe this motion, but we make two changes in notation: (1) we refer the motion to the vertical y axis with +y vertically up; (2) we replace a with -g, where g is the magnitude of the free-fall acceleration. Near Earth's surface, g = 9.8m/s2 (=32ft/s2)
|
Files:
| APCM Chapter 2 Presentation | |
| File Size: | 3034 kb |
| File Type: | ppt |
Skills Needed:
|
|