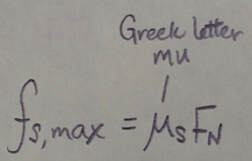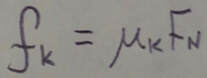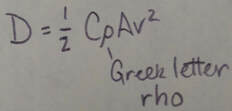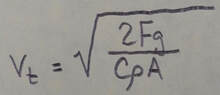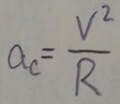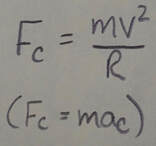Force and Motion II
|
Friction: When a force F tends to slide a body along a surface, a frictional force from the surface acts on the body. The frictional force is parallel to the surface and directed so as to oppose the sliding. It is due to bonding between the body and the surface.
If the body does not slide, the frictional force is a static frictional force f(sub)s. If there is sliding, the frictional force is a kinetic frictional force f(sub)k. 1. If a body does not move, the static frictional force f(sub)s and the component of F parallel to the surface are equal in magnitude, and f(sub)s is directed opposite that component. If the component increases, f(sub)s also increases. 2. The magnitude of f(sub)s has a maximum value f(sub)s,max given by: where mu(sub)s is the coefficient of static friction and F(sub)N is the magnitude of the normal force. If the component of F parallel to the surface exceeds f(sub)s,max, the body slides on the surface.
3. If the body begins to slide on the surface, the magnitude of the frictional force rapidly decreases to a constant value f(sub)k given by: where mu(sub)k is the coefficient of kinetic friction.
Drag Force: When there is relative motion between air (or some other fluid) and a body, the body experiences a drag force D that opposes the relative motion and points in the direction in which the fluid flows relative to the body. The magnitude of D is related to the relative speed v by an experimentally determined drag coefficient C according to:
|
where rho is the fluid density (mass per unit volume) and A is the effective cross sectional area of the body (the area of a cross section taken perpendicular to the relative velocity v).
Terminal Speed: When a blunt object has fallen far enough through air, the magnitudes of the drag force D and the gravitational force F(sub)g on the body become equal. The body then falls at a constant terminal speed v(sub)t, given by:
Uniform Circular Motion: If a particle moves in a circle or a circular arc of radius R at constant speed v, the particle is said to be in uniform circular motion. It then has a centripetal acceleration a with a magnitude given by:
This acceleration is due to a net centripetal force on the particle, with a magnitude given by:
where m is the particle's mass. The vector quantities a and F are directed toward the center of curvature of the particle's path.
|
Files:
| APCM Chapter 6 Presentation | |
| File Size: | 4035 kb |
| File Type: | ppt |